
0x00前言
本系列文章将带来cryptocals 这套密码学挑战的write-up.不同于通过上课或者看书的方式学习密码学,这些题目来自于现在生活中一些软件系统和密码构造中的缺陷。
本系列每一个题的wp基本是采用如下结构:题目解释、相关知识点讲解、代码实现及解释,运行测试。代码均采用python3实现,代码实现部分是参考国外大佬ricpacca的,结合自己的理解及成文需要进行部分修改。
第二套一共有八关。
第二套题目

主要是和分组密码相关的
0x01
先来看第9题
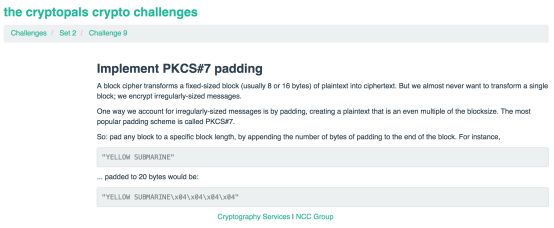
对于分组密码而言,通过会将整数的块的明文转为密文,但是我们一般碰到的消息长度不会是块的整数倍的,这时候就需要将其填充(padding)成块的整数倍大小。最流行的一种填充模式是PKCS#7
题目要求我们用代码实现PKCS#7
在分组加密算法中,进行分组时,划分后最后一组如果不够块大小时,需要填充,常见的填充模式有PKCS#5,PKCS#7。对于PKCS#5而言,明确定义Block的大小是8位,而在PKCS7Padding定义中,对于块的大小是不确定的,可以在1-255之间。
填充字符串由一个字节序列组成,填充的字节都是一个相同的字节,该字节的值就是要填充的字节的个数。
比如要填充7个字节,则需要填充7个0x7
实现一个函数,用于进行PKCS#7填充。如果消息长度等于块大小的话,无需填充,直接返回;否则先计算需要填充的长度,然后将其附加在原消息之后
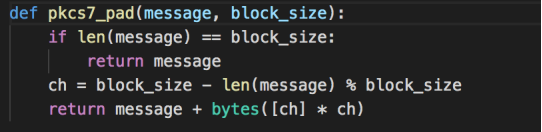
实现一个函数,用于判断数据是否经过PKCS#7填充。假设是正常实现的填充,将所填充的字符串存入padding,然后根据“填充的字节都是一个相同的字节,该字节的值就是要填充的字节的个数“进行检查。如果检查通过,则是经过PKCS#7填充的。

可以对应实现一个函数,实现逆PKCS#7填充,也就是将被填充的数据还原,通过is_pkcs_padded函数检查,如果没被填充过则直接返回,如果被填充过,则直接截取被填充后的字符串的前一部分(即原始数据)返回
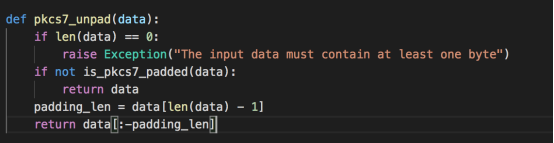
完整代码及执行结果如下
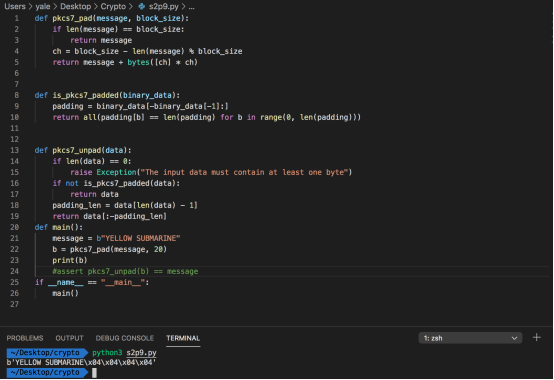
顺便使用断言测试pacs7_unpad是否可用
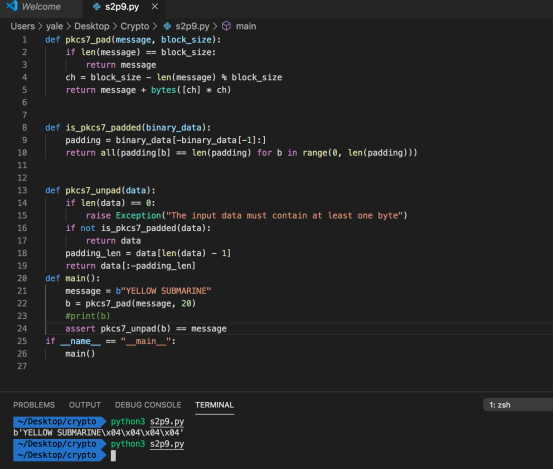
没有报错,说明正常执行
实验推荐--CTFCrypto练习之分组密码
(通过本实验的学习,你能够了解CTF竞赛中的密码学题型,掌握分组密码以及AES加密算法,学会分组密码ECB模式的攻击方法)
0x02
第10题

要求我们实现CBC模式,并对给出的文本文件进行解密。并提示我们复用之前写过的EBC代码(不过此时是写加密的函数)和XOR代码。还给出了密钥和IV
这里涉及的知识点是CBC模式
其中文全称是密码分组链接模式(Cipher Block Chaining (CBC))
这种模式是先将明文切分成若干小段,然后每一小段与初始块(IV)或者上一段的密文段进行异或运算后,再与密钥进行加密。如下所示
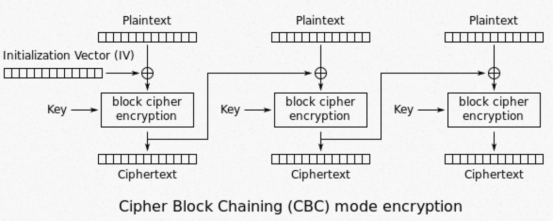
实现ASES-ECB加密函数。数据加密前常需要PKCS#7填充。

异或函数
![]()
实现AES-CBC加密函数,其接收的参数就是明文、密钥、IV
分块进行处理,分块后先进行填充padding,再进行与IV或上一个密文块进行异或,然后AES-ECB加密(即前面将CBC实现图中的加密器部分),接着处理下一块
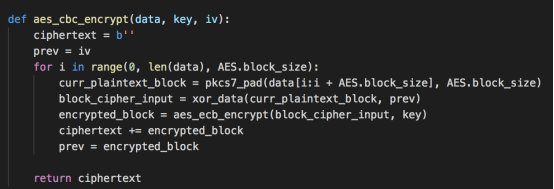
实现AES-CBC解密函数,可以返回填充或未填充的明文。同样需要分块进行,和加密函数倒着来就行,先AES-ECB解密,然后XOR。
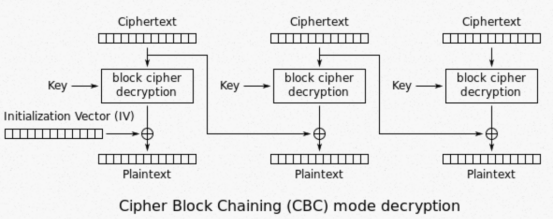
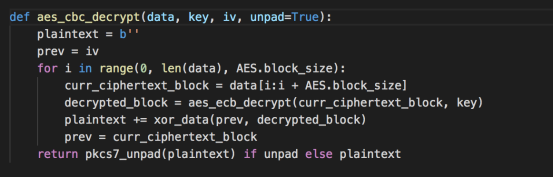
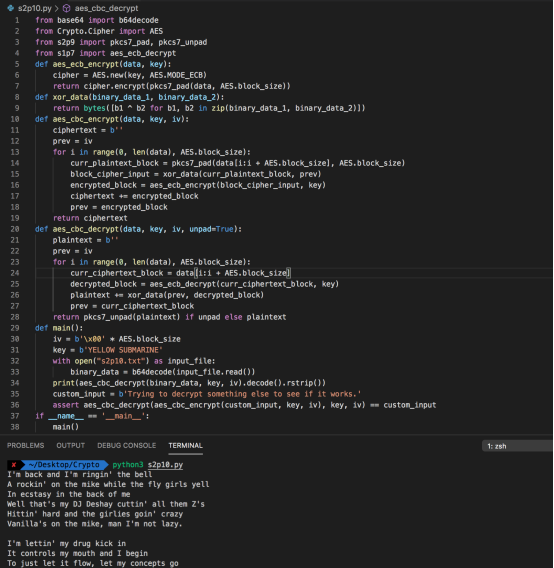
完整代码及执行后得到的明文如下
实验推荐--CBC字节翻转攻击
(通过该实验了解CBC模式实现流程、异或运算的高级应用、python中crypto库的使用以及cbc字节翻转攻击的原理与代码实现)
0x03
第11题

要求写一个函数实现生成随机的16字节AES 密钥
写一个函数根据随机密钥进行加密,在加密前在明文的前后各添加5到10字节随机值,随机选取加密方式为ECB或CBC,如果是CBC,还需要选择随机的IV
要求我们能够写一个函数,能够判断某个被加密的块是使用CBC还是ECB模式
根据填充后明文,随机生成的key,随机决定采用的模式(ECB或CBC)进行加密,如果是CBC的话,其IV也是随机的,所以用Random.new()
该数据填充上5到10字节随机数作为前缀和后缀
![]()
根据count_aes_ecb_repetitions返回的结果来判断是ECB还是CBC加密模式
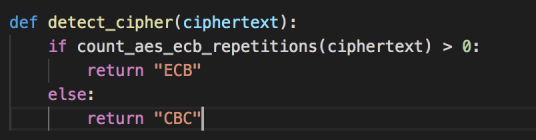
我们选择重复的输入数据,这样我们就可以结合ECB的特点来探测其是否为ECB模式,不是ECB则是CBC模式。
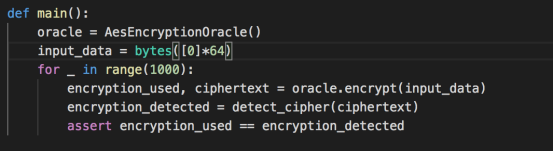
完整代码及执行断言结果如下
没有报错,说明写的这些函数都能成功执行。
0x04
第12题

该函数使用ECB模式,使用同一个但是未知的key
在加密前,在明文后附加给出的字符串(在附加之前先对该字符串base64解密我们有一个函数可以计算AES-128-ECB(your-string || unknown-string, random-key),而ECB Byte at a time技术可以让我们需要控制your-string,就可以在不知道random-key的情况下得到unkown-string。
基本流程如下:
1.将相同的字符串字节传入函数1,从传入1个字节(A)开始,然后AA,AAA。。。直到找到密文的块的大小
2.测试加密模式是否为ECB
3. 知道块的大小后,设计一个恰好少1字节的输入块(例如,如果块大小为8字节,则输入“ AAAAAAA”)。思考一下oracle函数将在最后一个字节位置放置什么。
4. 通过将不同的字符串输入到oracle中,为每个可能的最后一个字节创建字典;例如“ AAAAAAAA”,“ AAAAAAAB”,“ AAAAAAAC”,记住每个调用的第一个块。
5. 将one-byte-short输入的输出与字典中的一项匹配。 现在,我们就已经发现了unknown-string的第一个字节。
6.针对下一个字节继续重复
这里的原理还是基于ECB模式自身缺陷
假设我们有aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab,16字节分组后如下所示
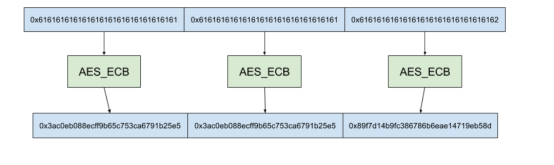
对于前两个块,他们的输入都是16个a,他们对应的输出是一样的。也就是说相同输入会有相同输出,我们就可以根据这一点进行攻击。
举个实际生活中的例子,假设找到一个网站,它的会话cookies是这么生成的:
AES_ECB(USERNAME + SECRET, KEY),我们作为攻击者可以任意改变username,得到不同的密文。作为攻击者,我们想要得到secret。来看看我们是怎么攻击的。
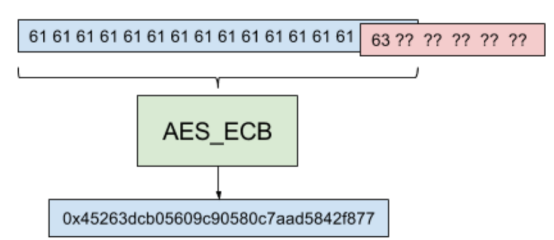
首先我们将15个a作为username,得到密文
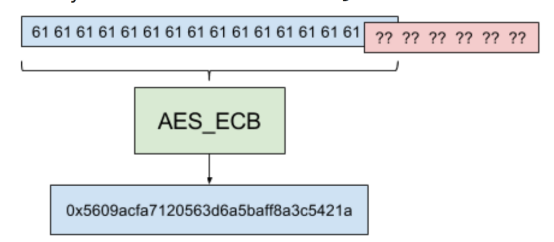
可知作为一个16字节大小的块,第16字节是来自secret的未知字符
接下来暴力测试第16个字节的可能值,将得到的相应密文与上图的密文对比
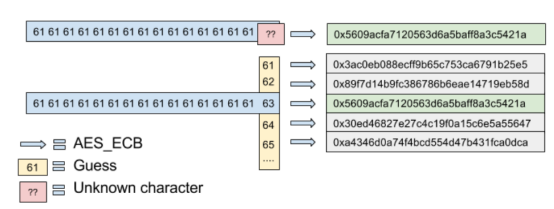
如上所示,当第16字节为c时,生成的密文和之前得到的密文是相同的,所以我们就知道secret的第1个字节是c了。
接下来我们设置username为14个a,则在构造块时,第15字节是secret的第一个字节c,那么第16个字节自然是来自secret的第二个字节,暂时未知,同样可以得到密文
然后暴力测试第16个字节的可能值
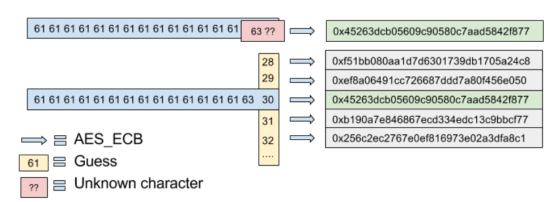
第16个字节为o时,密文才是一样的,所以可知secret的第二个字节为o
以此类推,就可以得到secret的明文了
回到题目本身,我们来看看如何实现
填充后使用AES-128-ECB模式加密

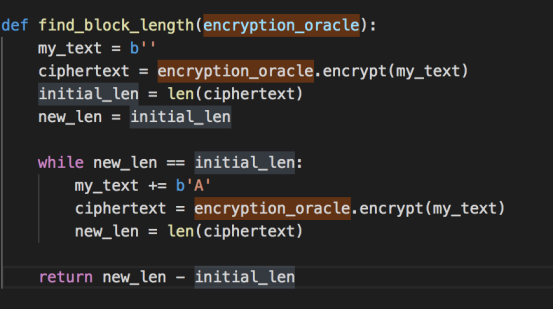
该函数用于返回encryption_oracle使用的块密码的块长度。
要找到一个块的长度,我们将加密越来越长的明文,直到输出密文的大小也增加为止。发生这种情况时,我们可以轻松地计算出一个块的长度,其值等于新的密文长度与其初始长度之间的差。
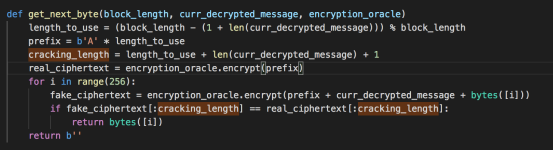
该函数用于获取依次获取unknown-string的下一个字节,这个函数是本题的关键。
首先计算要用作输入的字符数,以使unkown-string的第一个未知的字符置于块的末尾。接着计算我们从伪造的密文和实际密文得到的字节数,进行比较,这个值在后面的密文比较中用于截取数据。然后计算实际的密文。之后是暴力尝试,通过比较密文,来找到待求的字符
获取块长度,通过判断密文中是否有重复的字符串来判断是否为ECB模式。然后获取要解密的字符数量,其值等于我们加密空信息时得到的密文长度。该值在最后的循环中会用到,在循环体里,一个字符一个字符地操作。
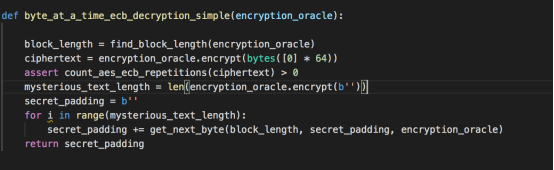
完整代码及执行结果如下:
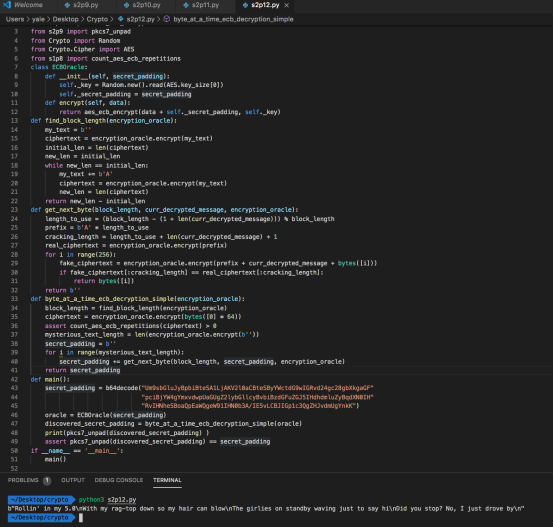
可以看到成功拿到了unknown_string的明文
也可以使用断言测试
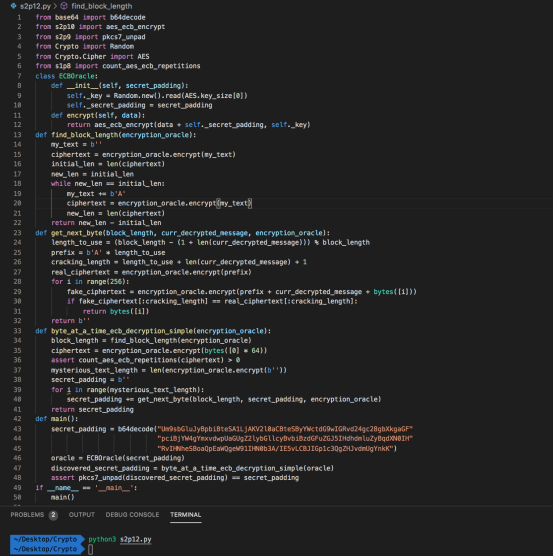
参考: